This mistake is a classic in my classroom. What does the student understand about combining like terms, but what is the conceptual model that makes this sort of mistake so enticing?
I would ask for each piece separately. What is close to? close to . What about ? Close to which is 7. So our answer should be close to 7. Is close to 7. This gives the student a chance to self-evaluate.
Then I would do factors for each part individually. Then we are back to is a banana, and we can add up our bananas at the end.
By the way,I find Runts candy to be very good as a source of bananas.
(hold breath for latex.)
Oops evidently I can do latex but can’t add. 3 plus 7 is about 10 usually. Stupid copy and paste. Sorry.
Bananas seems a bit odd to me here. If the student can do 3x – x correctly, then I would relate it back to that example, but I would be sure to call the variables bananas and not the irrational numbers bananas (my point is that the comment left by the teacher seems to assume a level of understanding that the student does not yet have). However, if the student can’t combine like terms (because 7sqrt(3) – 7sqrt(3) = 0 only demonstrates an understanding of the identity property of addition) then it may be a good idea to use whole numbers to develop an understanding. Also, it may be unclear that 3sqrt(7) is an expression of multiplication. Can the student estimate the value of 3sqrt(10)? If not, then using examples like 3(5) – 5 may help with 3x – x, but still not transfer to this problem.
3 replies on “A classic: Subtracting radicals”
I would ask for each piece separately. What is close to? close to
close to? close to 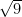 . What about
. What about  ? Close to
? Close to 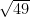 which is 7. So our answer should be close to 7. Is
which is 7. So our answer should be close to 7. Is 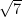 close to 7. This gives the student a chance to self-evaluate.
close to 7. This gives the student a chance to self-evaluate.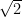 is a banana, and we can add up our bananas at the end.
is a banana, and we can add up our bananas at the end.
Then I would do factors for each part individually. Then we are back to
By the way,I find Runts candy to be very good as a source of bananas.
(hold breath for latex.)
Oops evidently I can do latex but can’t add. 3 plus 7 is about 10 usually. Stupid copy and paste. Sorry.
Bananas seems a bit odd to me here. If the student can do 3x – x correctly, then I would relate it back to that example, but I would be sure to call the variables bananas and not the irrational numbers bananas (my point is that the comment left by the teacher seems to assume a level of understanding that the student does not yet have). However, if the student can’t combine like terms (because 7sqrt(3) – 7sqrt(3) = 0 only demonstrates an understanding of the identity property of addition) then it may be a good idea to use whole numbers to develop an understanding. Also, it may be unclear that 3sqrt(7) is an expression of multiplication. Can the student estimate the value of 3sqrt(10)? If not, then using examples like 3(5) – 5 may help with 3x – x, but still not transfer to this problem.