When I talk about exponents, we go through a chart so they see the patterns:
3^3 = 27
3^2 = 9
3^1 = 3
3^0 = ???
3^-1 = 1/3
It boggles their mind still, but they understand it.
I was coming to see if anyone had already advocated the ‘reverse the number pattern in the table’ to define zero and negative integers as exponents yet … of course, friendly neighborhood Hemant (liked your response to the NY Times article by the way) beats me to it … I want to say I showed this to a college professor during my master’s work who mentioned during class that he didn’t know a good way to teach it to his remedial undergraduate students – made me feel a little better about all those times he had me confused
You ask, “Why should 2^0 = 0?” Doesn’t 2^3 mean 2 times itself 3 times? So then doesn’t 2^0 mean two times itself 0 times? Isn’t anything 0 times just nothing — zero? 2^0 = no 2s = 0.
How do we avoid the trap above when helping students make sense of 2^1, 2^2, 2^3, etc?
Remind students that every expression is multiplied by the understood 1. That makes the pattern a little easier.
You know, that just reminds me of what MIT be the problem. In that situation, we’re moving down the chart dividing by 3. So 3^0 is 3/3. Which…many students think is 0. For some reason. So it’s a division problem there.
I think that this idea is attractive because many students think that raising a number to a power is the same as multiplying the base by the power as in “4^2 = 8”
It seems like it should be true based on the way we explain raising to a power: 4^3 = three 4’s multiplied together, 4^2 = two 4’s multiplied together, 4^1 = one 4, 4^0 = zero 4’s… ??
The way that I’ve shown it (with varying success) is by showing that it’s consistent with the way we multiply/divide numbers with exponents
But I see 3^0 = 0 even from kids who have no trouble with 3^2 = 9. If that’s true of students in general, then there’s got to be more going on than just a kid thinking that bases should be multiplied by powers.
I really think it boils down to how difficult it can be for so many kids to make the transition from additive to multiplicative thinking. When you have an empty set of addends, then the nullary sum is zero, the additive identity. This makes total intuitive sense to kids: no addends = no sum. Hence nobody is really confused about why 4 x 0 = 0.
Things aren’t really any different when we have an empty set of factors instead. Then the nullary product is one, the multiplicative identity. But kids don’t think about the analogies between addition/additive identities and multiplication/multiplicative identities. They use the same intuition in both cases, so they think: no factors = no product. Unfortunately, in the additive case, “no sum” happens to coincide with the identity, the correct answer, but for the wrong reason. So when they try to reason about “no product,” they think zero, which is now the wrong answer, still for the wrong reason.
Really, I think students appeal to intuition to try to make sense of both 4 x 0 and 4^0, and they’re only accidentally right about the first one.
You know, I had honestly never thought of it like that. I can see a really useful compare/contrast activity coming from your comment. “kids don’t think about the analogies between addition/additive identities and multiplication/multiplicative identities.” They should though! I should! Hmmm. Thanks for the food for thought.
I want to “like” this comment.
Ahhh, this IS classic. During student teaching my students had major problems with this and I think it’s because I explained exponents like this: “if you have n^p, you’re multiplying the number n by itself p times.” Well, that works for positive, integer exponents but kinda sucks miserably for everything else.
I think I still might use the “multiplying a number by itself” thing but then ask students to try to figure out the rules for 0 and negative exponents based on patters. For example:
5^3= 5*5*5 = 125
5^2 = 5*5= 25 (or 125/5)
5^1 = 5*1 = 5 (or 25/5)
…. and then hopefully students see that if the pattern continues
5^0 = 5/5 =1
Then I’d have them do this for some more numbers to convince themselves.
After we talk about properties of exponents, namely that n^x/n^y = n^(x-y), I might even have them do a proof.
Great post. Was fun to think about.
Have you seen Keith Devlin’s protracted series “Multiplication is not repeated addition”? Here’s one place you could start
It is much more useful to view multiplication as “scaling”. Exponentiation demonstrates the effects of repeated scaling —- exponential growth or decay in size (start with 1 foot on July 1 and double it every day — on July 31, it’s almost the distance from the Earth to the Moon!) If you can get students to adopt the mentalities that exponentiation is related to multiplication and multiplication is scaling, I think it becomes easier to see what n^0 is.
For instance, Chris said above that it is hard to get students to think of the empty product as 1 instead of 0. If you view the empty product as “no scaling whatsoever”, it is not hard to convince someone that it should be 1 because scaling by a factor of 1 corresponds to no scaling.
You can also explain 0^0 in this framework. First, get them to believe that 0^n with n a positive integer is 0 (this part should be easy). Then talk about scaling by 0: it is much much stranger than scaling by a positive number. You can always “undo” scaling by a positive number, but not so with 0. Rather, 0 totally destroys the length you are scaling, and once that is accomplished, there would be no way for someone to recover the original length by scaling again. It is so strange that we should recognize the need to be careful with 0. If we believe 0^n is 0 when n is positive, then the pattern says 0^0 should be 0. However, you’ve presumably already discussed that for a positive (or maybe nonzero) base x, x^0 should be 1 (no scaling occurs). So to fit that pattern, 0^0 should be 1. Rather than make sense of the collision of these two patterns, the more common convention is to leave 0^0 undefined (although Max’s post below might be nice to throw in at this point).
Devlin also says in those pieces that exponentiation is not repeated multiplication, though.
One thing that I’ve tried — and this has been a mixed success, I think — has been by teaching exponents in the context of exponential functions. Here is how that works:
1. We start with everything to the right of the origin and we get an intuition for exponential growth, and situations where there would be exponential growth. So we start with doubling situations and population growth, and we extend from there into tripling and quadrupling situations. Then we learn how to write equations that describe these situations and graphs that we’ve developed. So kids are starting on firm footing with what means (i.e. start with 5000 and your double it 7 times).
2. “Hey, if means that you start with 5000 and double it 6 times, what does mean?
3. From there — and this is the weak part — I move to and we get an interpretation of that. We notice that is another way of saying “start with 1 and double it 6 times.”
4. Then we stick it with interpreting as “start with 1 and double it no times.”
5. Then on the next few quizzes I ask them to explain to an 8th grader why .
What’s good about this is that some kids end up with solid explanations of how to interpret zero exponents. I think a lot of kids think that this is somewhat annoying, though, so I need to figure out a way of spending less time explaining this stuff and more time giving them a chance to play with it in a way that’s useful.
Do you ever do any of the “does this break the rules of math?” explorations? Like, if students know that 2^3 * 2^5 = 2^(3+5), then have them decide whether 2^0 = 0 or 2^0 = 1 works better in 2^0 * 2^3 = 2^(0+3).
The table Hemant refers to is also a “how can we not break the rules of math?” argument I think.
I like the idea of developing it through functions, and wonder about sticking some “which of these definitions won’t break the rules of math?” in before #3?
Speaking of “breaking the rules of math,” the single most problematic part of this whole deal (even if it’s a small part, in the scheme of things) is trying to get at a sensible reason why 0 x 0 = 0, but 0^0 is undefined, because here even the analogy to multiplication breaks down. That’s really tricky for students, in my experience, even if you can get them to accept that n^0 = 1.
I’ve tried going with something like, “Well, 1 x 0 = 0, and if we remove an addend of zero, then we’re left with 0 x 0. Since ‘removing’ an addend of zero means subtracting 0, and since 0 – 0 is still zero, it follows that 0 x 0 = 0. If we start with 1^0 = 1 and remove a factor of one, then we’re left with 0^0. Since ‘removing’ a factor of zero means dividing by zero…wait, that’s a problem.” That’s not too terrible, but the reasoning from pattern like that doesn’t quite do away with the difficulty of, say, going from 3^0 = 1 and 2^0 = 1. Why doen’t that division by zero break the universe? This is a really, really frustrating topic from both sides of the desk. For me, anyway.
Ah…I meant “removing a factor of zero” in the second paragraph. Sorry…lunch break typing.
I love the use of context when developing exponential concepts!
Using paper folding as the context: 1 fold creates 2 layers, 2 folds creates 4 layers, 3 folds creates 8 layers . . . so #layers = 2^(#folds)
Next question: how many layers are there with zero folds?
You can also use the “Rice on a Chessboard” story. If you start with one grain on the first square, two grains on the second, four grains on the third, eight grains on the fourth. . . the rule becomes a bit trickier for the students: #grains = 2^(square# – 1) which again leads to 1 grain on the first square = 2^0.
These are the two exploratory lessons I have always used. The folding paper is supplemented by me telling them about the distance to the moon, etc; However… It would be even more valuable if I let them calculate thicknesses, find relative distances…. Oops, sorry, got a little off track!
I agree with you. 0 is the addition identity: 1 is the multiplication identity, so all exponentials are secretly multiplied by 1. If you multiply 1 by no factors, you get 1. You can of course add as many zeros as you like, but it doesn’t help.
What I like about 0^0 is it’s not even undefined, exactly. I mean, it’s controversial as to whether or not it’s defined (as 1) or undefined. Which is like meta-undefined, or un-undefined, or something. It’s a chance for students to see that math is unfinished, argumentative business, not a bunch of stuff that someone already knows and only sees fit to reveal in boring little packages.
Good point, Max. That last sentence, I think, gets at the heart of this whole thread. After all, shouldn’t our students have the chance to participate in the same kinds of discussions we’re having so much fun with? And aren’t they useful in deepening understanding, even when—maybe especially when—there’s disagreement?
The error that students make is quite logical when thought of in the context of positive exponents. What I have done in the classroom is work on developing the product and quotient of powers property using exponents in expanded form first, and then use the quotient of powers property and expended form to show that the case of a 2^0 would have to equal one. This method also helps explain the special case of 0^0 being undefined. Zero, (and negative) exponents still give most of my students fits.
This might be just a titch nit-picky, but I think it’s an important point. A few places in this thread, people have said something about the usual understanding of exponents (i.e., with positive integers) as , “a^b is a multiplied by itself b times.” We need to be super careful here. What we really mean is “a multiplied by itself b-1 times.” Like, b^2 is b times itself once. And b^3 is another multiplication by b (a second time). But we say it the other way a lot. Then kids say it. Then they start thinking of exponents as representing the number of multiplications instead of as the number of factors. Obviously this is a tough enough topic without adding more confusion, and kids definitely latch onto those kinds of phrases.
[…] Zero Exponents […]
The way that I tend to show this is through division. We take an example such as 10^2 / 10^2 and show that it leaves you with zero powers of ten. The students generally realise what is happening through cancellation. The other way is by using the charts shown above, but instead of using 3 to the power of something I always use 10 to the power of something as the pattern is much much easier to realise. Reinforce the chars with a division example and it is normal set for them.
The other point with regards to a^b being a multiplied by a b times. I never use that kind of thinking. With some of my pupils I will say the indices tells you how many of the number to write down the put multiplication symbols in there. E.g. 4^3 means write down 4 three times and then put multiply symbols between each one, we reinforce this. By using white boards and verbal examples.
[…] of these approaches were discussed in this comment thread on a post about a common exponent […]
[…] For a larger discussion of this issue, see this post from Math Mistakes. Share this:TwitterFacebookLike this:LikeBe the first to like this. This entry […]
[…] approaches: . Or . Once they have f(0), you can get ** For a larger discussion of this issue, see this post from Math Mistakes. Share this:TwitterFacebookLike this:LikeBe the first to like this. This entry […]
29 replies on “Classic: Zero exponents”
When I talk about exponents, we go through a chart so they see the patterns:
3^3 = 27
3^2 = 9
3^1 = 3
3^0 = ???
3^-1 = 1/3
It boggles their mind still, but they understand it.
I was coming to see if anyone had already advocated the ‘reverse the number pattern in the table’ to define zero and negative integers as exponents yet … of course, friendly neighborhood Hemant (liked your response to the NY Times article by the way) beats me to it … I want to say I showed this to a college professor during my master’s work who mentioned during class that he didn’t know a good way to teach it to his remedial undergraduate students – made me feel a little better about all those times he had me confused
You ask, “Why should 2^0 = 0?” Doesn’t 2^3 mean 2 times itself 3 times? So then doesn’t 2^0 mean two times itself 0 times? Isn’t anything 0 times just nothing — zero? 2^0 = no 2s = 0.
How do we avoid the trap above when helping students make sense of 2^1, 2^2, 2^3, etc?
Remind students that every expression is multiplied by the understood 1. That makes the pattern a little easier.
3^3 = 3*3*3*1 = 27
3^2 = 3*3*1 = 9
3^1 = 3*1 = 3
3^0 = 1
You know, that just reminds me of what MIT be the problem. In that situation, we’re moving down the chart dividing by 3. So 3^0 is 3/3. Which…many students think is 0. For some reason. So it’s a division problem there.
I think that this idea is attractive because many students think that raising a number to a power is the same as multiplying the base by the power as in “4^2 = 8”
It seems like it should be true based on the way we explain raising to a power: 4^3 = three 4’s multiplied together, 4^2 = two 4’s multiplied together, 4^1 = one 4, 4^0 = zero 4’s… ??
The way that I’ve shown it (with varying success) is by showing that it’s consistent with the way we multiply/divide numbers with exponents
But I see 3^0 = 0 even from kids who have no trouble with 3^2 = 9. If that’s true of students in general, then there’s got to be more going on than just a kid thinking that bases should be multiplied by powers.
I really think it boils down to how difficult it can be for so many kids to make the transition from additive to multiplicative thinking. When you have an empty set of addends, then the nullary sum is zero, the additive identity. This makes total intuitive sense to kids: no addends = no sum. Hence nobody is really confused about why 4 x 0 = 0.
Things aren’t really any different when we have an empty set of factors instead. Then the nullary product is one, the multiplicative identity. But kids don’t think about the analogies between addition/additive identities and multiplication/multiplicative identities. They use the same intuition in both cases, so they think: no factors = no product. Unfortunately, in the additive case, “no sum” happens to coincide with the identity, the correct answer, but for the wrong reason. So when they try to reason about “no product,” they think zero, which is now the wrong answer, still for the wrong reason.
Really, I think students appeal to intuition to try to make sense of both 4 x 0 and 4^0, and they’re only accidentally right about the first one.
You know, I had honestly never thought of it like that. I can see a really useful compare/contrast activity coming from your comment. “kids don’t think about the analogies between addition/additive identities and multiplication/multiplicative identities.” They should though! I should! Hmmm. Thanks for the food for thought.
I want to “like” this comment.
Ahhh, this IS classic. During student teaching my students had major problems with this and I think it’s because I explained exponents like this: “if you have n^p, you’re multiplying the number n by itself p times.” Well, that works for positive, integer exponents but kinda sucks miserably for everything else.
I think I still might use the “multiplying a number by itself” thing but then ask students to try to figure out the rules for 0 and negative exponents based on patters. For example:
5^3= 5*5*5 = 125
5^2 = 5*5= 25 (or 125/5)
5^1 = 5*1 = 5 (or 25/5)
…. and then hopefully students see that if the pattern continues
5^0 = 5/5 =1
Then I’d have them do this for some more numbers to convince themselves.
After we talk about properties of exponents, namely that n^x/n^y = n^(x-y), I might even have them do a proof.
Great post. Was fun to think about.
Have you seen Keith Devlin’s protracted series “Multiplication is not repeated addition”? Here’s one place you could start
http://www.maa.org/devlin/devlin_06_08.html
It is much more useful to view multiplication as “scaling”. Exponentiation demonstrates the effects of repeated scaling —- exponential growth or decay in size (start with 1 foot on July 1 and double it every day — on July 31, it’s almost the distance from the Earth to the Moon!) If you can get students to adopt the mentalities that exponentiation is related to multiplication and multiplication is scaling, I think it becomes easier to see what n^0 is.
For instance, Chris said above that it is hard to get students to think of the empty product as 1 instead of 0. If you view the empty product as “no scaling whatsoever”, it is not hard to convince someone that it should be 1 because scaling by a factor of 1 corresponds to no scaling.
You can also explain 0^0 in this framework. First, get them to believe that 0^n with n a positive integer is 0 (this part should be easy). Then talk about scaling by 0: it is much much stranger than scaling by a positive number. You can always “undo” scaling by a positive number, but not so with 0. Rather, 0 totally destroys the length you are scaling, and once that is accomplished, there would be no way for someone to recover the original length by scaling again. It is so strange that we should recognize the need to be careful with 0. If we believe 0^n is 0 when n is positive, then the pattern says 0^0 should be 0. However, you’ve presumably already discussed that for a positive (or maybe nonzero) base x, x^0 should be 1 (no scaling occurs). So to fit that pattern, 0^0 should be 1. Rather than make sense of the collision of these two patterns, the more common convention is to leave 0^0 undefined (although Max’s post below might be nice to throw in at this point).
Devlin also says in those pieces that exponentiation is not repeated multiplication, though.
One thing that I’ve tried — and this has been a mixed success, I think — has been by teaching exponents in the context of exponential functions. Here is how that works:
1. We start with everything to the right of the origin and we get an intuition for exponential growth, and situations where there would be exponential growth. So we start with doubling situations and population growth, and we extend from there into tripling and quadrupling situations. Then we learn how to write equations that describe these situations and graphs that we’ve developed. So kids are starting on firm footing with what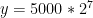 means (i.e. start with 5000 and your double it 7 times).
means (i.e. start with 5000 and your double it 7 times). means that you start with 5000 and double it 6 times, what does
means that you start with 5000 and double it 6 times, what does 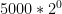 mean?
mean? and we get an interpretation of that. We notice that
and we get an interpretation of that. We notice that 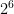 is another way of saying “start with 1 and double it 6 times.”
is another way of saying “start with 1 and double it 6 times.” as “start with 1 and double it no times.”
as “start with 1 and double it no times.”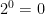 .
.
2. “Hey, if
3. From there — and this is the weak part — I move to
4. Then we stick it with interpreting
5. Then on the next few quizzes I ask them to explain to an 8th grader why
What’s good about this is that some kids end up with solid explanations of how to interpret zero exponents. I think a lot of kids think that this is somewhat annoying, though, so I need to figure out a way of spending less time explaining this stuff and more time giving them a chance to play with it in a way that’s useful.
Do you ever do any of the “does this break the rules of math?” explorations? Like, if students know that 2^3 * 2^5 = 2^(3+5), then have them decide whether 2^0 = 0 or 2^0 = 1 works better in 2^0 * 2^3 = 2^(0+3).
The table Hemant refers to is also a “how can we not break the rules of math?” argument I think.
I like the idea of developing it through functions, and wonder about sticking some “which of these definitions won’t break the rules of math?” in before #3?
Speaking of “breaking the rules of math,” the single most problematic part of this whole deal (even if it’s a small part, in the scheme of things) is trying to get at a sensible reason why 0 x 0 = 0, but 0^0 is undefined, because here even the analogy to multiplication breaks down. That’s really tricky for students, in my experience, even if you can get them to accept that n^0 = 1.
I’ve tried going with something like, “Well, 1 x 0 = 0, and if we remove an addend of zero, then we’re left with 0 x 0. Since ‘removing’ an addend of zero means subtracting 0, and since 0 – 0 is still zero, it follows that 0 x 0 = 0. If we start with 1^0 = 1 and remove a factor of one, then we’re left with 0^0. Since ‘removing’ a factor of zero means dividing by zero…wait, that’s a problem.” That’s not too terrible, but the reasoning from pattern like that doesn’t quite do away with the difficulty of, say, going from 3^0 = 1 and 2^0 = 1. Why doen’t that division by zero break the universe? This is a really, really frustrating topic from both sides of the desk. For me, anyway.
Ah…I meant “removing a factor of zero” in the second paragraph. Sorry…lunch break typing.
I love the use of context when developing exponential concepts!
Using paper folding as the context: 1 fold creates 2 layers, 2 folds creates 4 layers, 3 folds creates 8 layers . . . so #layers = 2^(#folds)
Next question: how many layers are there with zero folds?
You can also use the “Rice on a Chessboard” story. If you start with one grain on the first square, two grains on the second, four grains on the third, eight grains on the fourth. . . the rule becomes a bit trickier for the students: #grains = 2^(square# – 1) which again leads to 1 grain on the first square = 2^0.
These are the two exploratory lessons I have always used. The folding paper is supplemented by me telling them about the distance to the moon, etc; However… It would be even more valuable if I let them calculate thicknesses, find relative distances…. Oops, sorry, got a little off track!
I agree with you. 0 is the addition identity: 1 is the multiplication identity, so all exponentials are secretly multiplied by 1. If you multiply 1 by no factors, you get 1. You can of course add as many zeros as you like, but it doesn’t help.
What I like about 0^0 is it’s not even undefined, exactly. I mean, it’s controversial as to whether or not it’s defined (as 1) or undefined. Which is like meta-undefined, or un-undefined, or something. It’s a chance for students to see that math is unfinished, argumentative business, not a bunch of stuff that someone already knows and only sees fit to reveal in boring little packages.
See: http://mathforum.org/dr.math/faq/faq.0.to.0.power.html
Good point, Max. That last sentence, I think, gets at the heart of this whole thread. After all, shouldn’t our students have the chance to participate in the same kinds of discussions we’re having so much fun with? And aren’t they useful in deepening understanding, even when—maybe especially when—there’s disagreement?
The error that students make is quite logical when thought of in the context of positive exponents. What I have done in the classroom is work on developing the product and quotient of powers property using exponents in expanded form first, and then use the quotient of powers property and expended form to show that the case of a 2^0 would have to equal one. This method also helps explain the special case of 0^0 being undefined. Zero, (and negative) exponents still give most of my students fits.
This might be just a titch nit-picky, but I think it’s an important point. A few places in this thread, people have said something about the usual understanding of exponents (i.e., with positive integers) as , “a^b is a multiplied by itself b times.” We need to be super careful here. What we really mean is “a multiplied by itself b-1 times.” Like, b^2 is b times itself once. And b^3 is another multiplication by b (a second time). But we say it the other way a lot. Then kids say it. Then they start thinking of exponents as representing the number of multiplications instead of as the number of factors. Obviously this is a tough enough topic without adding more confusion, and kids definitely latch onto those kinds of phrases.
[…] Zero Exponents […]
The way that I tend to show this is through division. We take an example such as 10^2 / 10^2 and show that it leaves you with zero powers of ten. The students generally realise what is happening through cancellation. The other way is by using the charts shown above, but instead of using 3 to the power of something I always use 10 to the power of something as the pattern is much much easier to realise. Reinforce the chars with a division example and it is normal set for them.
The other point with regards to a^b being a multiplied by a b times. I never use that kind of thinking. With some of my pupils I will say the indices tells you how many of the number to write down the put multiplication symbols in there. E.g. 4^3 means write down 4 three times and then put multiply symbols between each one, we reinforce this. By using white boards and verbal examples.
[…] of these approaches were discussed in this comment thread on a post about a common exponent […]
[…] For a larger discussion of this issue, see this post from Math Mistakes. Share this:TwitterFacebookLike this:LikeBe the first to like this. This entry […]
[…] approaches: . Or . Once they have f(0), you can get ** For a larger discussion of this issue, see this post from Math Mistakes. Share this:TwitterFacebookLike this:LikeBe the first to like this. This entry […]