I’m thinking this student is solving (x-2)^2 like (x-2)(x-2) and then setting the quantities equal to 0 to get x=2.
Agreed. So many students look at y=ax^2+bx+c and 0=ax^2+bx+c as completely identical. Or if they just have ax^2+bx+c they will create an “=0” all on their own.
Many teachers and texts encourage this terrible habit, in the way problems are phrased or abbreviated.
This kid can’t factor, though.
I thought just , so obviously . Then y=4, evidently in the absence of any other information. I am much more impressed at the large quantity of intersection points, none of which contain the value
The y-intercept of their graph corresponds to one equation and the x-intercept of their graph corresponds to the other equation. The first three points of intersection are points on the line they graphed. They then took the “short cut” of figuring if (3,-2) & (4,-4) are on their line, so is (3+2, -2 + -4).
My main concern would be whether this student “knows” that quadratic equations produce parabolas? Then I would want to know whether it was just the y = 4 that is causing confusion – would they have done better with an equation like y = 3x + 1 instead.
I feel like the student recognized vertex form and latched on to something s/he knew — how to find the vertex — and then plotted that point.
6 replies on “Graphing Equations”
I’m thinking this student is solving (x-2)^2 like (x-2)(x-2) and then setting the quantities equal to 0 to get x=2.
Agreed. So many students look at y=ax^2+bx+c and 0=ax^2+bx+c as completely identical. Or if they just have ax^2+bx+c they will create an “=0” all on their own.
Many teachers and texts encourage this terrible habit, in the way problems are phrased or abbreviated.
This kid can’t factor, though.
I thought just
, so obviously 
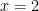. Then y=4, evidently 
in the absence of any other information. I am much more impressed at the large quantity of intersection points, none of which contain the value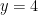 
The y-intercept of their graph corresponds to one equation and the x-intercept of their graph corresponds to the other equation. The first three points of intersection are points on the line they graphed. They then took the “short cut” of figuring if (3,-2) & (4,-4) are on their line, so is (3+2, -2 + -4).
My main concern would be whether this student “knows” that quadratic equations produce parabolas? Then I would want to know whether it was just the y = 4 that is causing confusion – would they have done better with an equation like y = 3x + 1 instead.
I feel like the student recognized vertex form and latched on to something s/he knew — how to find the vertex — and then plotted that point.