It looks to me like the student has seen the formula for the “average value of a continuous function over an interval [a,b]”: the average is 1/(b-a) times the integral of f over the interval [a,b]
I can think of no other reason why the student would introduce the symbol from the Fundamental Theorem of Calculus and then evaluate. Students often have problems understanding that this average is different from other averages they have seen. For instance, the average of a collection of numbers is (at first glance) quite different. Throw in “the average rate of change” as being (f(b)-f(a))/(b-a), and you’ve got a recipe for confusion.
Of course, the work above is nowhere near correct for computing “the average value of V’ over the interval [5,8]”, which indeed would just reduce to the correct formula (V(8)-V(5))/(8-5) when using the Fundamental Theorem of Calculus to compute it. Somehow I doubt the student would recognize that both methods would give the same answer, even if he/she is familiar with both.
I don’t think this is just a “mistake” — I think it’s a kid who doesn’t understand the difference between a derivative and an integral. It looks to me to be rather like the behavior of a kid who sees a word problem as “blah blah blah 8 blah blah blah 5 blah blah” and then guesses that the answer is probably one of 8-5, 8+5, 8*5, or 8/5, and maybe looks to the words a bit to see which one might be plausible. Here, they see “rate of change” so they think “derivative”, and they see the numbers 8 and 5 so they evaluate the derivative there, and then maybe they’re still thinking “change” so they subtract.
I would ask the student how to find average rate of change of ( , ) to ( , ) and then ask if the student can find the y values for this instance.
(I can only hope this LaTex thing works… as always )
That might get the student back on the right track.
I agree, Louise. Since “this is calculus” the student sees rate of change and automatically thinks “derivative!” Unfortunately, I am not sure they really understand the *concept* of rate of change, and certainly not the difference between average rate of change and instantaneous rate of change.
I also think a graphical approach might be helpful. Create some “story graphs” with time as the independent variable and have the student (or the whole class!) calculate and/or estimate the average rate of change over a specific interval and the instantaneous rate of change at a specific point in time. Then look at equations and ask the same questions – emphasize at least *thinking* about the graph when responding to the questions.
4 replies on “Rate of change”
It looks to me like the student has seen the formula for the “average value of a continuous function over an interval [a,b]”: the average is 1/(b-a) times the integral of f over the interval [a,b]
I can think of no other reason why the student would introduce the symbol from the Fundamental Theorem of Calculus and then evaluate. Students often have problems understanding that this average is different from other averages they have seen. For instance, the average of a collection of numbers is (at first glance) quite different. Throw in “the average rate of change” as being (f(b)-f(a))/(b-a), and you’ve got a recipe for confusion.
Of course, the work above is nowhere near correct for computing “the average value of V’ over the interval [5,8]”, which indeed would just reduce to the correct formula (V(8)-V(5))/(8-5) when using the Fundamental Theorem of Calculus to compute it. Somehow I doubt the student would recognize that both methods would give the same answer, even if he/she is familiar with both.
I don’t think this is just a “mistake” — I think it’s a kid who doesn’t understand the difference between a derivative and an integral. It looks to me to be rather like the behavior of a kid who sees a word problem as “blah blah blah 8 blah blah blah 5 blah blah” and then guesses that the answer is probably one of 8-5, 8+5, 8*5, or 8/5, and maybe looks to the words a bit to see which one might be plausible. Here, they see “rate of change” so they think “derivative”, and they see the numbers 8 and 5 so they evaluate the derivative there, and then maybe they’re still thinking “change” so they subtract.
I would ask the student how to find average rate of change of ( ,
,  ) to (
) to ( 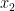 ,
,  ) and then ask if the student can find the y values for this instance.
) and then ask if the student can find the y values for this instance.
(I can only hope this LaTex thing works… as always )
That might get the student back on the right track.
I agree, Louise. Since “this is calculus” the student sees rate of change and automatically thinks “derivative!” Unfortunately, I am not sure they really understand the *concept* of rate of change, and certainly not the difference between average rate of change and instantaneous rate of change.
I also think a graphical approach might be helpful. Create some “story graphs” with time as the independent variable and have the student (or the whole class!) calculate and/or estimate the average rate of change over a specific interval and the instantaneous rate of change at a specific point in time. Then look at equations and ask the same questions – emphasize at least *thinking* about the graph when responding to the questions.