What’s the nature of this student’s mistake? Is it the sort of mistake that the kid would make given a linear equation to solve, or is the mistake particular to the trig context? How might you help the kiddo?
The student doesn’t understand why you are allowed to perform the same operation to both sides of an equation. Show the student that 8+4*3=20, but if you repeated their first step, you’d change this to the false statement 8+3=5. Explain to the student that equalities are statements that two different looking expressions are actually the same number, just written in two different ways (or occasionally in the same way!). If you’ve written a number in two different ways, and if you then square root both expressions or divide both by 4, you’ll still have the same number written twice. Then indicate to the student that he didn’t divide the whole expression on the left by 4, and he later didn’t take the square root of the whole expression on the left.
One problem with given writing sample is that sin(x) = 0 ends up being one of the solutions. If the student is particularly hard-headed, he’ll think that since he got “a right answer”, his method was perfectly fine and you’re just being a tyrant by demanding that it be done “your way”. Go through the student’s same work replace the 0 on the right with a 12. The student would then find that sinx = sqrt{3}/2, so x is a multiple of 2pi plus either pi/3 or 2pi/3. Point out that neither of these is solutions of the original equation. Then emphasize that the student completely lucked out in arriving at numbers that actually are a few of the solutions.
None of these issues have anything to do with trig. I’d go back to quadratics and ask for Then you can substitute in for y.
2 replies on “Solving quadratic trig equations”
The student doesn’t understand why you are allowed to perform the same operation to both sides of an equation. Show the student that 8+4*3=20, but if you repeated their first step, you’d change this to the false statement 8+3=5. Explain to the student that equalities are statements that two different looking expressions are actually the same number, just written in two different ways (or occasionally in the same way!). If you’ve written a number in two different ways, and if you then square root both expressions or divide both by 4, you’ll still have the same number written twice. Then indicate to the student that he didn’t divide the whole expression on the left by 4, and he later didn’t take the square root of the whole expression on the left.
One problem with given writing sample is that sin(x) = 0 ends up being one of the solutions. If the student is particularly hard-headed, he’ll think that since he got “a right answer”, his method was perfectly fine and you’re just being a tyrant by demanding that it be done “your way”. Go through the student’s same work replace the 0 on the right with a 12. The student would then find that sinx = sqrt{3}/2, so x is a multiple of 2pi plus either pi/3 or 2pi/3. Point out that neither of these is solutions of the original equation. Then emphasize that the student completely lucked out in arriving at numbers that actually are a few of the solutions.
None of these issues have anything to do with trig. I’d go back to quadratics and ask for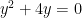
Then you can substitute in for y.