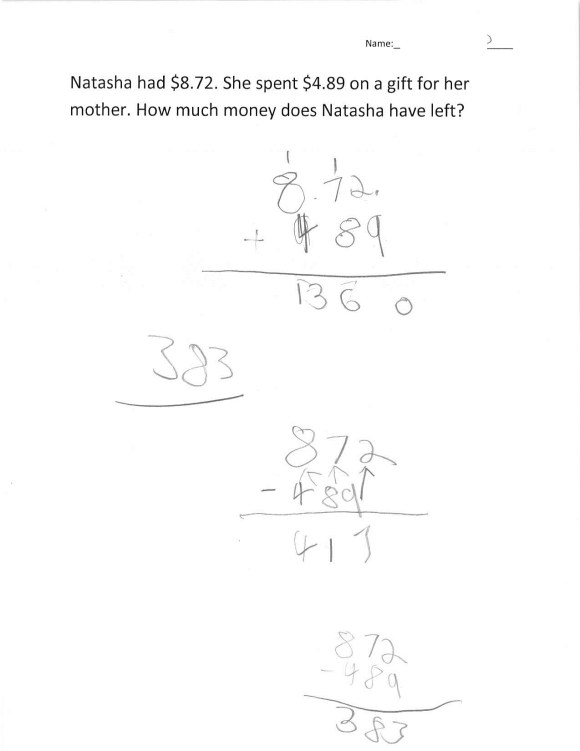Natasha had $8.72. She spent $4.89 on a gift for her mother. How much money does Natasha have left?
- I gave this question to my 4th Grade class. (11 kids, one absent.) It was December, I had seen them do a variety of subtraction work. I knew that a lot of them could handle subtraction using something like the standard algorithm — though certainly not everyone — and I was wondering whether a money context would be easier or harder for them. Would you predict that $8.72 – $4.89 would be easier or harder than 872 – 489?
- What approaches would you predict kids to take for this money problem? What mistakes do you expect to see?
Take a look below, and then report back in the comments:
- Which student’s approach surprised you the most?
- Assume that you’ve got time in the curriculum to ask students to work on precisely one question at the beginning of class the next day. What question would you ask to address some of the ideas you see in their work below?
Student 1
Student 2
Student 3
Student 4
Student 5
Student 6
Student 7
Student 8
Student 9
Student 10