
I want to share a theory on this mistake:
The student had an association between negative exponents and reciprocals and “half-powers” and square roots. As the student was parsing the problem he “fulfilled his obligation” to use that association on the number. I guess what I’m positing is that the mind works by making a connection, and then remaining in tension until that connection is used in a problem. (I’ve often had the experience of feeling as if there’s an insight that I haven’t used yet in solving a problem, and it’s like having a small weight on my back.) The mind comes to relief at the moment that the insight is used.
The student’s mind made the connection between negative powers and reciprocals and was in tension. He then used this insight at the first opportunity he saw, to relieve himself from the burden of his insight.
Some of you might disagree. For instance, you might think that the student had just memorized some rule poorly, had no conceptual understanding of powers, and gave the answer that he did.
But I think that the answer felt right because he used the fact that he knew. I’d predict that this student would be able to answer 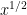 correctly.
correctly.
If you think that the student just memorized a rule, is there any reason to think that a student would get a question such as 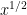 correct?
correct?























