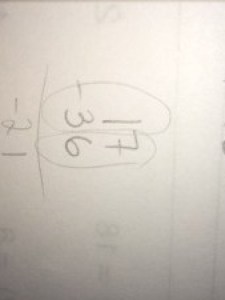
Seeing this everywhere across all grades. Anyone have ideas? #MTBoS #mathchat pic.twitter.com/vt9xlj5Bxj
— Justin (@JustinAion) May 22, 2017
Nobody asked me, but here’s my thought.
When people learn something new, they cling to a paradigmatic case. This paradigmatic image matters more for how they use this new idea than whatever rules or logic they might otherwise adhere to. For example, when kids are first learning about triangles, they don’t identify new triangles on the basis of properties. They look at their paradigmatic image of triangle and compare this new shape to it. This is why kids misidentify so many shapes, at first. Below, 10 might be declared a triangle, though 5 would be rejected.
Now, it would be sort of besides the point to lament young children’s tendency to identify shapes in this way. This is just what the beginning of the learning curve looks like. It helps teachers to be familiar with this tendency — we can directly address it in friendly ways — but it’s totally normal. In particular, it’s not really an artifact of instruction.
(I suppose if kids make it to a weirdly old age without being able to logically identify triangles, yeah, that would be an artifact of instruction.)
I think the situation with square roots that Justin points out is pretty similar to this. When kids solve equations by taking the square roots of both sides, a lot a lot of these cases involve a square root solution. It seems totally normal for kids to start seeing this as a paradigmatic case, and to think that all solutions to such equations involve square roots. Totally normal, not something to stress too much about.
In fact, I saw this mistake in my 8th Grade class last week. A kid was using the Pythagorean Theorem, and had put little square roots over the side lengths. No stress: told him that this wasn’t necessary; reminded him of the conceptual meanings that made this move incorrect; reminded myself to include more chances for him to practice this idea; set him off to try the next problem, but without the extra square roots.
I think this is just how learning happens.
I’ve sometimes read or talked to teachers who wished kids didn’t make these sorts of mistakes. And I guess it would be nice if kids could just reach an age where they operated as logical, analytical and meaning-oriented students at the start of their learning curves. I understand why we teachers feel a bit of nervousness when kids aren’t being guided by meaning.
But ‘being guided by meaning’ is another way of saying ‘being guided by logic,’ and this is not my understanding of how beginners hold on to new ideas.
It’ll take time, practice, corrections, maybe a big ol’ worksheet, but if a kid made it that far in solving these equations, they’ll make it the rest of the way. Keep it up!