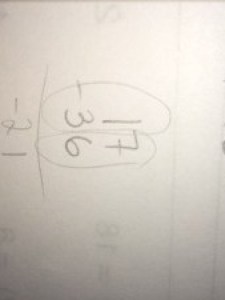
I know, I know what you’re thinking. I even know what you’re about to say. “Oy! These kids, just being taught algorithms which they blindly follow without reasoning. They even sometimes can’t even remember the algorithm! This poor kid doesn’t remember the algorithm correctly. He thinks that what he/she is supposed to do is subtract the smaller number from the larger number. Boo procedural thinking.”
Or, maybe you see this and think: “This kid isn’t even thinking. Just operating blindly on numbers. A shame, really…”
A third option: “This kid learned an incorrect rule. This kid thinks that what you’re supposed to do is subtract the smaller number from the larger number.”
Each of these explanations, I think, is a little bit off.
- The first and the third theory make predictions about what a student “thinks is right.” What could this mean, if not that the student, when asked, would say what they did was correct? But I think that students, when prompted to reflect on this work, would quickly identify the mistake.
- The second theory predicts that the student, when prompted, couldn’t explain how to properly subtract any double-digit numbers with understanding. I’m be willing to put down money that this kid, when presented with 54 – 32, could explain how to do this with as much understanding as your average kid.
We need some language and distinctions to properly describe what’s going on here.
- The kid wasn’t thinking slowly, deliberately, explicitly. He wasn’t under the sway of a procedure or a concept.
- He was just doing math, not thinking about the math he was doing. He was going with the flow, doing what seemed like it should be done.
This puts us in opposition to all three of the above theories:
- The kid didn’t have an explicit algorithm that he was trying to follow. He wasn’t under its sway.
- The student wasn’t just operating blindly and randomly on the numbers. He wasn’t guessing. He was doing the math without thinking about doing the math, though.
- The kid didn’t have a mistaken concept of subtraction. He wasn’t under the sway of any particular concept. He was just doing what needed to be done.
There was a mistake here? Or a misconception? Or a false belief in a bad procedure? How exactly should we describe this?
- Objectively speaking, it is a mistake. The word “mistake” doesn’t refer to a person’s thinking, but rather refers fairly objectively to the result of their thinking. Objectively speaking, this was a mistake. The kid said something that wasn’t true.
- But there’s no evidence here of a misconception. A misconception has to do with concepts, and this kid wasn’t under the direction of any mistaken concepts. He understands what subtraction is. He understands what place value is. He could tell you about them.
- It’s not a false belief, because there’s no evidence here that this kid believes that what he did is correct.
- It’s not a dumb mistake, something that happens randomly and without thought.
Instead, maybe we should call this a mental bias, or a tendency towards this sort of mistake. This problem has revealed an underlying bias in this kid’s tendency to subtract a smaller number from the larger number. What’s revealed is a sort of magnetic urge to take away a smaller number from a larger one, rather than a larger one from a smaller one.
What do we do about those sorts of tendencies? I think that a certain kind of practice is called for, but I’m not sure. Thoughts on that? On any of this?
6 replies on “Trying Out Some Language For The Causes of Mistakes”
I believe Kahneman language in “Thinking Fast and Slow” might be very well suited (confession: I’m still less than halfway through his book). I’d say that this student was using more of “System 1” than “System 2” when deciding how to approach this problem.
Now this is seemingly ironic, since Kahneman uses multiplying two two-digit numbers as a prime example as a sort of task that immediately puts us in “System 2”. And most students DO put themselves in “System 2” mode when executing procedures like the one above. I think, though, that many students only put themselves in that mode until they’ve already decided how to approach the problem, that is, they decide the approach based on instinct, then start thinking hard about executing the approach correctly. I think many also immediately switch it off when the procedure is done, precluding important finishing work like deciding if the answer is sensible or reflecting on other approaches they might have used. Perhaps a combination of math anxiety and/or the general amount of taxation mathematical thinking requires makes it natural to want leave System 2 on for as short a time as possible. Feel free to tear apart this theory, but I still think Kahneman’s ideas are terrifically relevant here.
From Howard Phillips http://www.howardat58.wordpress.com
It looks to me that the student does not understand “subtraction” in the signed number system.
He thinks that it is still “take away”.
Someone needs to explain that in the signed number system the numbers, both positive and negative, are not measures of quantity, but measures of position and also positive and negative movements.
19 – 36 therefore means “how far is it from 36 to 19 (on a numberline if that helps)”,
or “where do I end up if I start at 17 and move 36 steps to the left”.
He should have a few questions like
“It is -10 degrees here in Alaska and 81 degrees in Miami. What id the difference in temperature?”
or
“It was 22 degrees here this afternoon. By midnight the temperature had fallen by 31 degrees. What was the temperature at midnight?”.
and so on.
One of the reasons for this failure to “get it” is that for years kids are told that subtraction is “take away” , and there is little or no attempt to see subtraction in the natural numbers as also “finding the difference between”.
I like trying to tease this out. Maybe there is a possibility that there is a misconception as to how the standard algorithm carries out subtraction? The student understands the connection between difference and subtraction. But overall, I agree that most misapplied algorithms fall into mistake or not yet understanding.
I actually think this student is closer to understanding that perhaps this work would indicate. If shown an alternative algorithm like partial sums, it would be easy to show that indeed 7-6 = 1 (as indicated) AND that 1-3 (representing 10-30 if accurately showing place value) = -20. Now just combine those partial results -20 + 1 = -19, the correct result.
i’d have to have somehow noticed that a particular student makes (even if somehow vaguely) *this kind* of mistake before i’d think about what might be going on with that student’s “understanding”. on its face, it looks like a classic “careless error”… one that its author will be able to fix merely upon having it pointed out. but i *do* consider this “trying out language about errors” to be a *very* valuable exercise. for teachers. we usually shouldn’t try to get *students* whatever language we come up with, though, i think. far too often in beginner-math, teachers end up presenting ill-understood philosophical models *in place of* perfectly-clear-when-taken-seriously definitions (or, for that matter, procedures). this seems to be one of the major reasons nobody can compute with fractions around here, for example.
/*we usually shouldn’t try to get *students* whatever language we come up with,*/
i garbled this. luckily, i never tire of reading my own prose. it should of course read
“… try to get *students* to use whatever language…”. thank you and good day.