What’s up with the above? Say something smart in the comments about the implications of a mistake like this one. What’s another mistake that you would expect this student to make in the future? What’s a mistake that you wouldn’t expect the student to make?
Thanks to Jonathan Newman for the submission.
5 replies on “Combining Like Powers”
Notation hurricane. How do we get students in trig who haven’t processed this yet?
I see a student blindly sticking to left to right (o/w they “cancel” +tan^4-tan^4), and interpreting an exponent as ‘how many of the base are there?’ Probably helped by the unfamiliar context of the trig functions and how we abuse exponentiation notation with those. Also “no” coefficient on the functions to tip off that there are two quantities involved here.
Of course, this speaks to a student not having full and completely understood when you can add exponents, when you can combine like terms, etc.
But I think it also speaks to how contextual so much of learning is. I would bet that this kid would never combine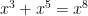
. Of course, if he really understood why he shouldn’t do that then he wouldn’t do that with the trig functions either. But I wonder if it’s just a context that throws him off of what he’s learned (shallowly), and that this is how we get kids in trig who can’t get this straight.
Ask students what they think the difference between tan^2x and tanx^2 and (tanx)^2. Spending some time on notation and identifying it in problem solving could be helpful. There’s also the distribution error, maybe the student is doing too many steps at once. Another reason why it’s important to teach patient and careful problem solving.
Recently I saw somewhere that you’d introduced your students to the idea of f^4(x) being f(f(f(f(x)))). That seemed great because it leads to f^(-1)(x) not being division but inversion which is excellent.
But then they’ll get here where tan^2(x) is not tan(tan(x)). Ugh. Our notations don’t always do our learners any favors.
I’d wonder how this student immediately wrote down that sec^4(x) is (1+tan^2(x))^2 which is almost as non-obvious as the proof that is being asked for. (Though perhaps it was the result of problem 2). Then I wonder if the notation issues have them wavering about whether the ^2 is some kind of special notation that only applies to these trig functions (which, in a way, it is…)
Now you can post my comment to formattagclosingmistakes.org ! I won’t mind.