I’d love to hear anything that you’re thinking about this in the comments.
I wonder: should we be giving kids explicit guides for these sorts of algorithms at all? Algorithms ought to be patterns in thought. Does a mistake like this begin to make a case against these sort of printed aids?
Thanks to Professor Triangleman for the submission.
14 replies on “Lattice versus Partial Products”
Let’s ask CCSS to answer your questions.
Fourth grade: fluently add and subtract using the traditional algorithm.
Fifth grade: fluently multiply using the traditional algorithm.
Sixth grade: fluently divide using the standard algorithm.
I’m pretty concerned that the student didn’t notice that there are two different answers for the same problem. An emphasis on the Practices would help in this classroom.
I agree that the student probably saw two different problems. Why should we expect the same answer? To the student, this wasn’t “Lattice versus Partial Products” at all, in that case… just two different squiggle requests… I wonder if this was a strictly visual process (which I see fairly often at teh college age level with students at this “skill” level), which would speak against providing the “printed aid.”
To be fair, the student in question *did* notice the two different answers, which led to my noticing them, which led to a photograph and the submission to math mistakes.
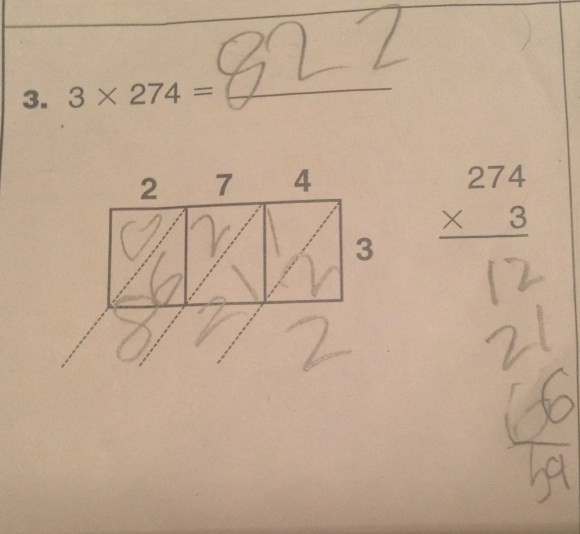
From my perspective, this is an elegant example of Constance Kamii’s claim that algorithms unteach place value. The task was to do a set of multiplication problems two ways—once with the lattice algorithm, and once with the partial products algorithm. The lattice (like the CCSS-mandated standard algorithm) implores us not to think about place value as we work. Therein lies efficiency. But efficiency is at the cost of thinking.
I am not the teacher in the classroom in question here, so I cannot say how this error, and others like it, gets dealt with. As parent of this guy, I used his noticing that the answers didn’t match (by a lot!) to turn the conversation towards place value. Is 7×3 in this problem really seven times 3? We agreed that it was 7 tens times 3, which is 21 tens, or 210. Et cetera.
The contrast became a good learning opportunity.
But I do find it troubling that the abstraction of the lattice led to mistakes in the partial products algorithm, rather than the other way around. That is, I would much rather that the boy wonder where the 210 in the partial products algorithm disappears to in the lattice.
“The Standard Algorithm” is undefined by design. It was a CCSS compromise. The “Smart Guys” advocate 39×56 by the use of partial products and 397×569 with a calculator. There are VERY GOOD reasons to do it this way.
In some versions of the Partial Products algorithm, students are taught to write the partial products with all the relevant 0s at each step. Even if they have a semi-mindless rule to follow about how many 0s to put down, it would still be good to give them at least some chance of seeing the partial products with the proper place value notation. And counting on young kids to line up zeroless partial products properly seems to be a risky idea. (Which leads to the suggestion that they should do all this work on grid paper with one digit per box, and boxes sized appropriately for their age.)
This is probably not the place to raise this question, but I’ll do it anyway. You write “Therein lies efficiency.” But why are we teaching them this? If you want efficiency, use a calculator.
Partial products show the distributive property. This is easily shown in 2×2 arrays. More than that: use a calculator.
Neither method puts enough emphasis on place value or the distributive property. I prefer the rectangle method – exactly the same idea often used to introduce polynomial multiplication. Remove the diagonals from the lattice, write 200 instead of 2 and 70 instead of 7. Fill the boxes with 600, 210, and 21. More skills required to use this method, but what is the point of multiplying by hand if you cannot do things like 3 x 200 mentally?
If you have not looked at any of James Tanton’s stuff, you should. The rectangle method is one of many great ideas I found looking through his sight.
In the CCSS, this is called arrays and is the visual representation of partial products
I agree, the area model is a great one for understanding multiplication, though a little slow because it can be a lot of extra writing especially when the numbers get more digits.
I like the area model so much, I asked my friend Dave Millar to draw a multiplication table to scale: http://thegriddle.net/educators (Multiplication Table Handout on that page).
Use calculators for everything past 2×2 arrays.
Looking at this, my first thought is that the student did the lattice first (one of my least fav methods), where the digits are separated to not denote place value and put the answers in the boxes. Moved on to the partial products and transcribed the same products from the lattice. When the answers don’t match, I agree with Christopher, it opens up an interesting conversation about place value.
Teaching K-5, it is always interesting to hear my 3rd graders doing number talks where they are mentally solving problems like the one above with place value reasoning, it just makes sense to them with no “steps” or “rules”, just thinking about the numbers. Then move to a 5th grade classroom where they are solving the same problem incorrectly with an algorithm someone has taught them. I do not think algorithms are bad necessarily, but I do think there is such a foundation that needs to be built with place value understanding. When teachers jump too quickly to the algorithm, the common sense of the problem is lost.
Lets stop kidding ourselves, this is just a bloated load of crap and proof that our education system is not only broken (we already know that) but they have completely lost touch with reality! The standard algorithm for solving simple math are far and above the best method and one that translates well when working with other forms of math. The kids would have much better results if they counted on their fingers. Whoever came up with the partial products method needs to have their head examined. If our kids cannot multiply simple equations using known methods that work and end up with correct answers then I think it is time we started questioning the ability of the teachers. I have never been more disgusted with how my kid is learning than I am right now, WHAT A JOKE!
Hey Kevin — thanks for writing.
I’m a math teacher, and experience + things I’ve read make me suspicious of written algorithms altogether. In other words, it’s hard for me to get too excited about either partial products or the standard algorithm.
The truth is, in 99% of my adult contexts, if I have a calculation that needs to be done on pencil and paper, it’s going to be faster and more accurate for me to pull out my phone and do a short calculation.
But mental math? That stuff’s golden. Being able to quickly calculate stuff in your head helps out a ton in life, and it also makes learning other math easier (since you don’t get distracted by numbers when you’re learning, say, some algebra).
The problem is that the standard algorithm is completely useless as a mental algorithm. It’s only good on paper. We need a whole host of other strategies for doing mental math, and (fortunately) there’s a lot of good research and materials for improving kids mental math abilities.
I basically agree with this post: http://nicoraplaca.com/mental-math/
Oh, also, the tone around here is usually a bit more congenial FYI.