The proof above isn’t great. In the comments, take on any of the following questions (or any others):
- Sometimes kids slap stuff together when they’re confused, and other times they’re substantively mistaken. Which is this, and what evidence supports your position?
- How would you help this student recognize that the logic in his proof doesn’t flow?
- What would your next steps be in working with this student? What sorts of problems would you ask him/her to solve?
- From the picture above, what evidence of knowledge do we have?

5 replies on “Problems with Proofs”
I don’t think that this proof was just slapped together out of confusion. There’s too much particular reference of non-obvious principles, and there’s too much confidence in the student’s presentation for this to just be random markings on a page. Instead, I think that there is a coherent argument here that the student doesn’t know how to express.
Any explanation of what the student was thinking will have to explain the following: ?
? along with the partition postulate? Shouldn’t he just have written “given”?
along with the partition postulate? Shouldn’t he just have written “given”?
1. Why did the student think it important that
2. Why did the student think it important to rewrite
3. What’s the deal with the reflexive property?
4. What’s the deal with invoking vertical angles at the end?
I think that I can nail 1, 2 and 4.
I think the kid was trying to prove that , and then using supplementary angles to finish the proof. “Verticals” is a confusion between “vertical angles” and “supplementary angles.” The mention of the partition postulate is meant to earn the fact that
, and then using supplementary angles to finish the proof. “Verticals” is a confusion between “vertical angles” and “supplementary angles.” The mention of the partition postulate is meant to earn the fact that 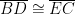 for use in proving that
for use in proving that 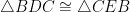 .
.
If this is right, then what’s cool about this mistake is that the problem is almost entirely in the form and terminology used in the proof. There’s an entirely coherent argument, and the issues that the student needs to work through have to do with vocabulary and explaining thought through proof. It’s not an issue with the student’s congruent triangles knowledge, so it would be a mistake for the teacher to go down that road with the student.
So — does anyone think that this is a problem with the student’s knowledge about triangles and angle theorems? Do you think the student is just placing random markings on the page? Do you think that you can give a better explanation of the student’s thinking? What’s going on with the reflexive property here?
I think the student is trying to say that the bisectors are of necessity perpendicular, and so equal.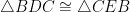 , if I had this student, I would continue with the angle bisectors and ask about the bisector of angle A, because the dashed line can then go through the intersection I of the other two bisectors, and can then have the
, if I had this student, I would continue with the angle bisectors and ask about the bisector of angle A, because the dashed line can then go through the intersection I of the other two bisectors, and can then have the  . These two triangles don’t overlap, so it is sometimes easier for students to see. Plus, it does not negate any of the work they have done, although it might not be the neatest solution.
. These two triangles don’t overlap, so it is sometimes easier for students to see. Plus, it does not negate any of the work they have done, although it might not be the neatest solution.
Without looking for
I don’t buy it. I don’t think the student had much understanding or a plan.
The first thing that needs to be made clear is how to recognize vertical angles. I like to hold up my arms and show that X. The students can then visualize the non-adjacent angles formed by the X.
Before reading any of the comments, I thought maybe the student was aiming for . That’s why it becomes important that
. That’s why it becomes important that  and
and 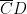 both bisect the base angles B and C– because then
both bisect the base angles B and C– because then  .
.  becomes important to restate now, although this is where I’m less sure my route is the route the student was aiming for– s/he could have been headed towards an AAS proof but is missing that
becomes important to restate now, although this is where I’m less sure my route is the route the student was aiming for– s/he could have been headed towards an AAS proof but is missing that 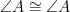 , or could have been headed towards the nonexistent SSA proof (since we have
, or could have been headed towards the nonexistent SSA proof (since we have 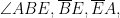 and its corresponding parts on the other triangle).
and its corresponding parts on the other triangle).
My explanation, however, does not at all account for the reflexive .
.