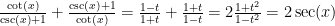In the comments: can you reconstruct each step of the student’s argument? What was he thinking?
Thanks to Kristen Fouss for the submission.
[We have a growing library of trig identities, and I’ve got like 10 more trig identities to post over the next few weeks. Seems to be a tough spot for students.]

8 replies on “Trig Identities”
That’s not an identity problem, that’s fractions. He seems pretty solid on the identities.
Maybe I’m missing something, but I think there are some trig issues as well. The student’s work claims that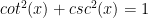 (in the move from the 1st line in pencil to the 2nd line in pencil).
(in the move from the 1st line in pencil to the 2nd line in pencil).
Oops. Missed that. You’re right. I was focusing on the fraction errors, which are dismal considering it’s a trig student.
But trig is fractions – it’s why we are all over the elementary teachers who tell our kids they don’t need to know how to manipulate fractions. Can’t use a calculator for algebra 2 (can use Wolfram Alpha, though).
Um, yeah. I know trig is fractions.I also know that if you have a kid who can’t master fractions, teaching trig is amazingly pointless. So I was focusing on the fraction errors.
The student was thinking…
Step 1: Get a common Denominator.
Step 2: Gross, my numerator is a mess. Is there an identity to substitute to make it friendlier?
Step 3: Okay, I see csc(x) in the numerator and denominator, CANCEL!! Ooo, I can add those now.
Step 4: Factor of 2’s cancel.
Step 5: Dividing by cot(x) is silly, reciprocal of the reciprocal of tan(x), keep the 2 in front.
It’s Friday, I’m up for the LaTex lesson… Mike, if it’s wrong, please rescue me! and
and 
 assuming the Latex is right.
assuming the Latex is right. , thereby avoiding using the word canceling.
, thereby avoiding using the word canceling.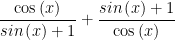
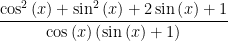
 gives us 1. So I wonder whether this little friend saw someone else’s work and copied badly.
gives us 1. So I wonder whether this little friend saw someone else’s work and copied badly.

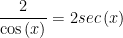
I’m old school, I only do
So I start with
So then I put
Now
Multiplying to a common denominator,
Now, look here, the
After that it was just fractions.
and then easily to
Latex is hard. http://www.quickmeme.com/meme/35945v/
The student knows that the trig identity must reduce to something simple (because that’s the type of problems that are always set). You can see all of the erased work where they tried other approaches and they only stopped in this last attempt since they got something simple – despite or because of the mistakes.
The mistakes and thinking have been well covered by the first three commenters, so here’s my version of a solution using Weierstrass substitution.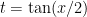 with
with  ,
, ,
,  .
.
Set
so
Substitute and simplify: