So this student is adding the number 2 in front of the radical to the 6. It’s one of those apples and oranges situations. I might ask this student to replace sort(5) with a variable, say r, and then ask them if they can simplify 2r+6.
By the way, we support LaTeX now, so you should be able to write , if you so desire.
My first reaction was that this is a classic combining like terms error. But then, I started thinking that this student could easily have that concept down, with the understanding that you need to “add the numbers together” and since these are both numbers, s/he added them.
On a related note, I’ve grown more and more disenchanted with the word “simplify” as I find it can be misleading to students, who then tend to want to get things down into one term. I’ve been working on trying to give a clear message about what “simplify” really means in a variety of contexts.
I’d love to hear/read more about how you get rid of the word “simplify.” In the context of rational expressions I made a little bit of progress on this problem by talking about “special 1s” and “factoring.” This post has a fuller explanation.
I tend to tell students that simplifying can only get so far… that the square root of five *is* a complicated thing. An awful lot of them think it’s a five… that they’re not allowed to treat like a five. I work at getting the idea across that the radical is like a division sign, and it means that the number is supposed to be divided by whatever number gives the same a nswer as the thing you divided by… and might eve say it’s irrational and ugly, and that six over there is just a nice, regular six that doesn’t want to get involved in any irrational behavior 😉
I think a mistake like this uncovers a weakness in the students understanding of “like terms”. If they only see like terms as numbers vs. letters then they need much more experience with varied kinds of terms. For example, can we get students to see that 4^2 + 4^2 is equal to 2(4^2)? Verbally it sounds something like “this is a four squared and this is a four squared so all together we have two four squared’s”
It’s really all about equivelency. How do we create equivalent expressions and how can we justify their equivelency?
This one problem is hitting multiple objectives, but if the true objective is “simplifying” radicals then maybe something like “Write an equivelent expression for 5(root 5) – 3(root 5) + 6” would yield more useful results.
I think this relates to a basic lack of understanding of “multiply”. 2\ital{x} is 2 “of those things” (like hats) so 2\sqrt{5} is two of those surd fives (or bananas). Clearly it would be silly to add hats and bananas together.
Sorry if the LaTeX does not work out: I’m a high school teacher and don’t usually use such highfalutin’ stuff.
All you have to do to get the LaTeX working is precede your code with “$latex” and end it with ” $”.
Also, this is relevant to a lot of what people are talking about: The Banana Rule
Please forgive me I am going to try the LaTeX instructions $latex2\sqrt{5}$
nope still not right (sigh) failing this class do I need open close arrows like html tags?
oh, I also need spaces. If anyone else is learning, use dollar latex then space then the LaTeX code then a space then a dollar sign.
Thank you all for your patience. And Mr P for being a kind teacher.
12 replies on “Adding Radicals”
So this student is adding the number 2 in front of the radical to the 6. It’s one of those apples and oranges situations. I might ask this student to replace sort(5) with a variable, say r, and then ask them if they can simplify 2r+6.
By the way, we support LaTeX now, so you should be able to write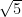 , if you so desire.
, if you so desire.
My first reaction was that this is a classic combining like terms error. But then, I started thinking that this student could easily have that concept down, with the understanding that you need to “add the numbers together” and since these are both numbers, s/he added them.
On a related note, I’ve grown more and more disenchanted with the word “simplify” as I find it can be misleading to students, who then tend to want to get things down into one term. I’ve been working on trying to give a clear message about what “simplify” really means in a variety of contexts.
I’d love to hear/read more about how you get rid of the word “simplify.” In the context of rational expressions I made a little bit of progress on this problem by talking about “special 1s” and “factoring.” This post has a fuller explanation.
I tend to tell students that simplifying can only get so far… that the square root of five *is* a complicated thing. An awful lot of them think it’s a five… that they’re not allowed to treat like a five. I work at getting the idea across that the radical is like a division sign, and it means that the number is supposed to be divided by whatever number gives the same a nswer as the thing you divided by… and might eve say it’s irrational and ugly, and that six over there is just a nice, regular six that doesn’t want to get involved in any irrational behavior 😉
I think a mistake like this uncovers a weakness in the students understanding of “like terms”. If they only see like terms as numbers vs. letters then they need much more experience with varied kinds of terms. For example, can we get students to see that 4^2 + 4^2 is equal to 2(4^2)? Verbally it sounds something like “this is a four squared and this is a four squared so all together we have two four squared’s”
It’s really all about equivelency. How do we create equivalent expressions and how can we justify their equivelency?
This one problem is hitting multiple objectives, but if the true objective is “simplifying” radicals then maybe something like “Write an equivelent expression for 5(root 5) – 3(root 5) + 6” would yield more useful results.
I think this relates to a basic lack of understanding of “multiply”. 2\ital{x} is 2 “of those things” (like hats) so 2\sqrt{5} is two of those surd fives (or bananas). Clearly it would be silly to add hats and bananas together.
Sorry if the LaTeX does not work out: I’m a high school teacher and don’t usually use such highfalutin’ stuff.
All you have to do to get the LaTeX working is precede your code with “$latex” and end it with ” $”.
Also, this is relevant to a lot of what people are talking about: The Banana Rule
Please forgive me I am going to try the LaTeX instructions $latex2\sqrt{5}$
nope still not right (sigh) failing this class do I need open close arrows like html tags?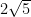
oh, I also need spaces. If anyone else is learning, use dollar latex then space then the LaTeX code then a space then a dollar sign.
Thank you all for your patience. And Mr P for being a kind teacher.