Last week we posted a somewhat similar mistake involving logarithms. Here’s the student work:
While you should feel free to comment on today’s mistake independent of the earlier one, I think it would be especially productive to compare these two pieces of student work. Could the same student have done both pieces of work? Are there differences between the way each student understands logarithms?
By the way, we now support equation editing in LaTeX, so feel free to write things such as in the comments. This post is also tagged with a Common Core Standard and categorized according the hierarchy that you see in the menu on the left.


5 replies on “Dividing by “log””
Here, this student has dropped the 2 in front of the first term, and didn’t cancel out the log. So if they’re thinking “just divide out the logs” they’ve made a mistake in simplifying.
In addition they still don’t seem to understand how to simplify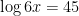 , so they don’t seem to have an understanding of the meaning of the logarithm. In the last problem, we didn’t know if a student could solve equations like
, so they don’t seem to have an understanding of the meaning of the logarithm. In the last problem, we didn’t know if a student could solve equations like  .
.
Usually when I get errors this severe, it isn’t just a misconception about logs. It is also about very poor algebra I equation solving skills, and poor work habits. This is much worse than the previous problem.
I think this problem goes deeper than logs. Something about how we teach functions leaves students unable to tell when f(a+b)=f(a)+f(b) holds true and when it doesn’t.
Can you say more? I’m not quite understanding you.
Couldn’t agree more! Square roots and rational expressions especially – root(x^2 + 9) becomes x + 3; x/(x + 5) becomes 1 + x/5 etc. I have pondered doing a more advanced order of operations unit that includes expressions with variables, log/ln, composition – exciting stuff, right? But, many students are not so clear about order of operations with numbers, let alone when variables are involved.