Dear Math Mistakes,
This piece of student work [below] puzzled us. What’s your take on what’s going on in the first one?
Sincerely,
Baffled at Ben-Gurion

***
For our readers who don’t speak Hebrew, here is my translation of the problems:
Three brothers received an inheritance.
A) The oldest brother received 72,600 shekels, which was 33% of the inheritance. What was the total amount of the inheritance?
B) The second brother received 37% of the inheritance. How much did he receive?
C) What percentage of the inheritance did the third brother receive? How much did the third brother inherit?
***
Dear Baffled,
Fascinating stuff!
From the second two problems, this student seems to have a solid procedure for finding a given percentage of an original amount. If asked to find 20% of 5000, this student would compute (20 * 5000)/100.
But what do you do when you don’t know the original amount? This is what the first problem calls for, since the total inheritance is the unknown. One way that a particularly sophisticated algebra student might approach this would be to solve the following equation: (33 x ?)/100 = 72600.
It seems to me that this student is trying very hard to head towards something like this sophisticated approach. They’re looking at (20 x 5000)/100 and trying to figure out how to invert the procedure, to solve for the original amount. Neither attempt really lands at anything accurate or workable, but you can see an attempt to make sense out of inverting a formula.
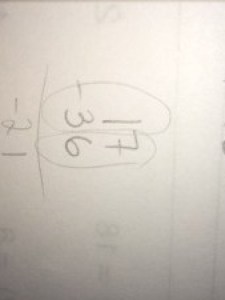
In that first attempt — I’m assuming it’s a first attempt — the student tries to put the brother’s inheritance at the bottom of the fraction and to insert the other two brothers’ percentage at the top of the fraction. Again, nothing truly sensical here, but you see three attempts at inversion — 67 instead of 33, multiplication by 100 instead of division by 100, and putting the inheritance in the bottom of the fraction.
In the second attempt the student tries to scale 72600 by (100 + 33) to uncover the original total inheritance. I see this as attempting something like scaling up the 72600, which is not a bad idea at all, but this is still being embedded in a larger attempt at inverting the “forwards” procedure.
(It also seems to me possible that this student tried to solve (33 x ?)/100 = 72600 for “?” and somehow mushed together the 33 and 100, but then I wouldn’t know where the 67 came from.)
What to make of all this? All that really matters for the student is what they can learn next, and engineering this is always the hard, context-dependent part of looking at student work. Based only on knowing this, though, I’d say that they could be ready to learn to solve (33 x ?)/100 = 72600 for “?.” There are other less algebraic ways to go about this, but it seems to me like this student could be ready for the algebraic approach.